Articles
See also on arXiv or MathSciNet.
Preprints
Publications
Solutions of a polynomial equation modulo a prime power
with Christian Drouin, to appear in American Math. Monthly
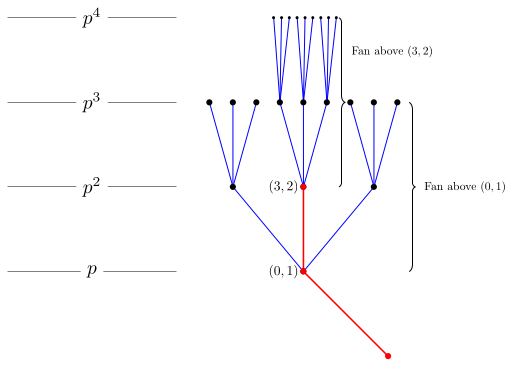
How do you find the integer solutions of a polynomial equation modulo an integer?
You will find at the bottom of this page the Sage code to compute these solutions.
Around the gcd of the values of two polynomials
with Christian Drouin, American Math. Monthly, 2025

We propose a mathematical walk around the gcd of the values A(n) and B(n) of two polynomials evaluated at an integer n. This is an opportunity to use a very powerful tool: the resultant.
Combinatorial study of morsifications of real univariate singularities
with Evelia Rosa García Barroso, Patrick Popescu-Pampu and Miruna-Stefana Sorea, Math. Nachrichten, 2024
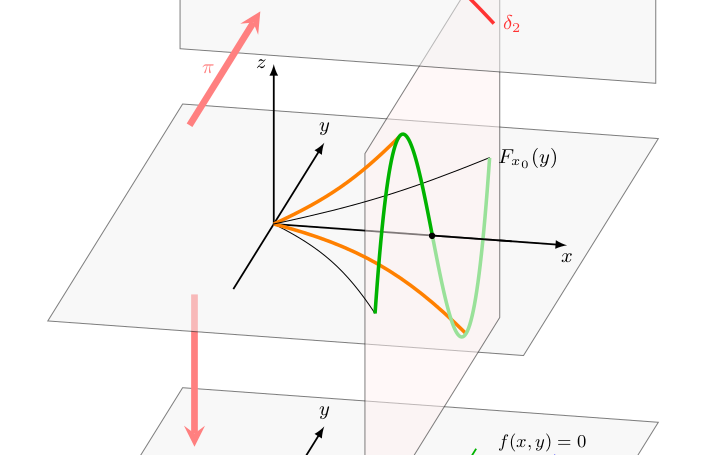
We study a broad class of morsifications of germs of univariate real analytic functions. We characterize the combinatorial types of the resulting Morse functions, via planar contact trees constructed from Newton-Puiseux roots of the polar curves of the morsifications.
Poincaré-Reeb graphs of real algebraic domains
with Patrick Popescu-Pampu and Miruna-Stefana Sorea, Revista Matemática Complutense, 2023
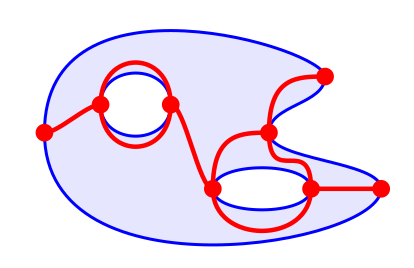
An algebraic domain is a closed topological subsurface of a real affine plane whose boundary consists of disjoint smooth connected components of real algebraic plane curves. We study the non-convexity of an algebraic domain by collapsing all vertical segments contained in it: this yields a Poincaré-Reeb graph, which is naturally transversal to the foliation by vertical lines. We show that any transversal graph whose vertices have only valencies 1 and 3 and are situated on distinct vertical lines can be realized as a Poincaré-Reeb graph.
Coprime values of polynomials in several variables
with P. Dèbes, Israel J. Math., 257, 2023

Given two polynomials P(x), Q(x) in one or more variables and with integer coefficients, how does the property that they are coprime relate to their values P(n), Q(n) at integer points n being coprime? We show that the set of all gcd (P(n), Q(n)) is stable under gcd and under lcm. A notable consequence is a result of Schinzel: if in addition P and Q have no fixed prime divisor (i.e., no prime dividing all values P(n), Q(n)), then P and Q assume coprime values at “many” integer points. Conversely we show that if “sufficiently many” integer points yield values that are coprime (or of small gcd) then the original polynomials must be coprime. Another noteworthy consequence of this paper is a version over the ring of integers of Hilbert’s irreducibility theorem.
The Hilbert-Schinzel specialization property
with P. Dèbes, J. König and S. Najib, Crelle’s Journal, 785, 2022

We establish a version “over the ring” of the celebrated Hilbert Irreducibility Theorem. Given finitely many polynomials in k+n variables, with coefficients in Z, of positive degree in the last n variables, we show that if they are irreducible over Z and satisfy a necessary “Schinzel condition”, then the first k variables can be specialized in a Zariski-dense subset of Z^k in such a way that irreducibility over Z is preserved for the polynomials in the remaining n variables. The Schinzel condition, which comes from the Schinzel Hypothesis, is that, when specializing the first k variables in Z^k, the product of the polynomials should not always be divisible by some common prime number. Our result also improves on a “coprime” version of the Schinzel Hypothesis: under some Schinzel condition, coprime polynomials assume coprime values. We prove our results over many other rings than Z, e.g. UFDs and Dedekind domains for the last one.
Bilipschitz equivalence of polynomials
Mathematische Nachrichten, 294, 2021
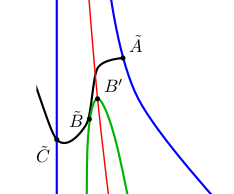
We study a family of polynomials in two variables having moduli up to bilipschitz equivalence: two distinct polynomials of this family are not bilipschitz equivalent. However any level curve of the first polynomial is bilipschitz equivalent to a level curve of the second.
The Schinzel hypothesis for polynomials
with P. Dèbes and S. Najib, Transaction AMS, 373, 2020

The Schinzel hypothesis is a famous conjectural statement about primes in value sets of polynomials, which generalizes the Dirichlet theorem about primes in an arithmetic progression. We consider the situation that the ring of integers is replaced by a polynomial ring and prove the Schinzel hypothesis for a wide class of them: polynomials in at least one variable over the integers, polynomials in several variables over an arbitrary field, etc. We achieve this goal by developing a version over rings of the Hilbert specialization property. A polynomial Goldbach conjecture is deduced, along with a result on spectra of rational functions.
Prime and coprime values of polynomials
with P. Dèbes and S. Najib, L’enseignement mathématique, 66, 2020

The Schinzel Hypothesis is a celebrated conjecture in number theory linking polynomials and prime numbers. In the same vein, we investigate the common divisors of values of polynomials and establish a “coprime Schinzel Hypothesis”. We deduce a version “modulo an integer” of the original Hypothesis, and as special cases, the Goldbach conjecture and the Twin Primes conjecture, again modulo an integer.
Intermediate links of plane curves
with M. Borodzik, Israel J. Math., 227, 2018
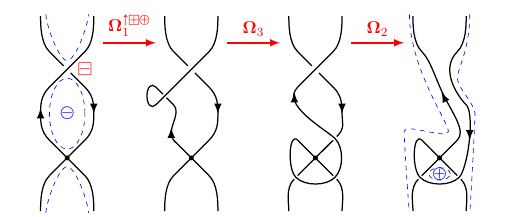
For a smooth complex curve we consider the link Lr obtained by intersecting the curve with a sphere of radius r. We prove that the diagram Dr obtained from Lr by a complex stereographic projection satisfies topological equalties. As a consequence we show that if Dr has no negative Seifert circles and Lr is strongly quasipositive and fibered, then the Yamada–Vogel algorithm applied to Dr yields a quasipositive braid.
Families of polynomials and their specializations
with P. Dèbes and S. Najib, J. Number Theory, 170, 2017
For a polynomial in several variables depending on some parameters, we discuss some results to the effect that for almost all values of the parameters the polynomial is irreducible. In particular we recast in this perspective some results of Grothendieck and of Gao.
The braid group of a necklace
with P. Bellingeri, Math. Z., 283, 2016
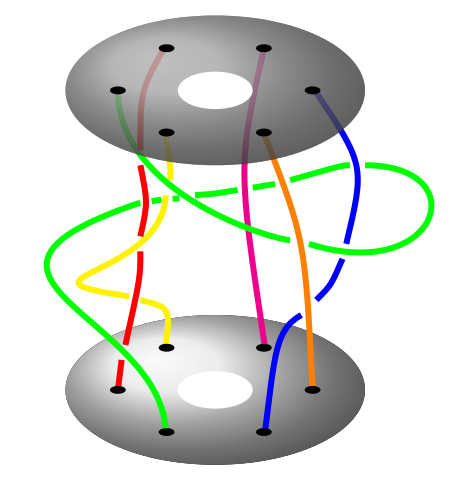
We study several geometric and algebraic properties of a necklace: a link composed with a core circle and a series of circles linked to this core. We first prove that the fundamental group of the con- figuration space of necklaces is isomorphic to the braid group over an annulus. We then defne an action on the fundamental group of the configuration space of the necklaces to the automorphisms of the free group and characterize these automorphisms among all automorphisms of the free group.
Topology of generic line arrangements
Asian J. of Math., 19, 2015
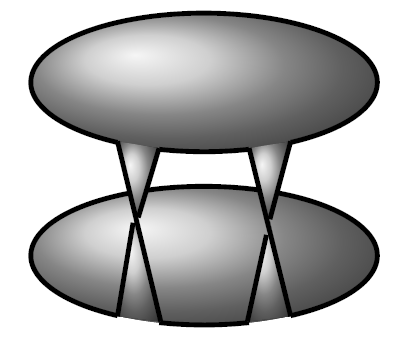
Our aim is to generalize the result that two generic complex line arrangements are equivalent. In fact for a line arrangement A we associate its defining polynomial f= prod_i (a_ix+b_iy+c_i), so that A= (f=0). We prove that the defining polynomials of two generic line arrangements are, up to a small deformation, topologically equivalent. In higher dimension the related result is that within a family of equivalent hyperplane arrangements the defining polynomials are topologically equivalent.
Waring problem for polynomials in two variables<
with Mireille Car, Proc. American Mathematical Society, 141, 2013
We prove that all polynomials in several variables can be decomposed as the sum of k-th powers: P(x_1,…,x_n) = Q_1(x_1,…,x_n)^k+ … + Q_s(x_1,…,x_n)^k, provided that elements of the base field are themselves sum of k-th powers. We also give bounds for the number of terms s and the degree of the Q_i^k. We then improve these bounds in the case of two variables polynomials to get a decomposition P(x,y) = Q_1(x,y)^k+ … + Q_s(x,y)^k with deg Q_i^k less than deg P + k^3 and s that depends on k and ln(deg P).
Specializations of indecomposable polynomials
with Guillaume Chèze and Pierre Dèbes, Manuscripta Mathematica, 139, 2012
We address some questions concerning indecomposable polynomials and their behaviour under specialization. For instance we give a bound on a prime p for the reduction modulo p of an indecomposable polynomial P(x) in Z[x] to remain indecomposable. We also obtain a Hilbert like result for indecomposability: if f(t_1,…,t_r,x) is an indecomposable polynomial in several variables with coefficients in a field of characteristic p=0 or p>deg(f), then the one variable specialized polynomial f(t_1+a_1 x,…,t_r+a_r x,x) is indecomposable for all (t_1,…, t_r, a_1,…,a_r) i the closure of k^{2r} off a proper Zariski closed subset.
Integral points on generic fibers
J. London Mathematical Society, 81, 2010
Let P(x,y) be a rational polynomial and k in Q be a generic value. If the curve (P(x,y)=k) is irreducible and admits an infinite number of points whose coordinates are integers then there exist algebraic automorphisms that send P(x,y) to the polynomial x or to x^2-dy^2, d in N. Moreover for such curves (and others) we give a sharp bound for the number
Decomposition of polynomials and approximate roots
Proc. American Mathematical Society, 138, 2010
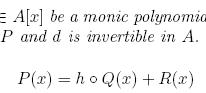
We state a kind of Euclidian division theorem: given a polynomial P(x) and a divisor d of the degree of P, there exist polynomials h(x),Q(x),R(x) such that P(x) = h(Q(x)) +R(x), with deg h=d. Under some conditions h,Q,R are unique, and Q is the approximate d-root of P. Moreover we give an algorithm to compute such a decomposition. We apply these results to decide whether a polynomial in one or several variables is decomposable or not.
See the library at the end of this page for examples of computations.
Generating series for irreducible polynomials
Finite Fields and Applications, 16, 2010
We count the number of irreducible polynomials in several variables of a given degree over a finite field. The results are expressed in terms of a generating series, an exact formula and an asymptotic approximation. We also consider the case of the multi-degree and the case of indecomposable polynomials. See the examples of computations below.
- Milnor fibrations of meromorphic functions
with José Seade and Anne Pichon, Journal of the London Mathematical Society, 80, 2009 - Indecomposable polynomials and their spectrum
with Pierre Dèbes and Salah Najib, Acta Arithmetica, 139, 2009 - Irreducibility of hypersurfaces
with Pierre Dèbes and Salah Najib, Communications in Algebra, 37, 2009 - Number of irreducible polynomials over finite fields
American Mathematical Monthly, 115, 2008 - Jump of Milnor numbers
Bull. Braz. Math. Soc., 38, 2007 - Reducibility of rational functions
Israel Journal of Mathematics, 164, 2008 - Meromorphic functions, bifurcation sets and fibred links
with Anne Pichon, Mathematical Research Letters, 14 ,2007 - Topological equivalence of polynomials
with Mihai Tibar, Advances in Mathematics, 199, 2006 - Computation of Milnor numbers and critical values at infinity
Journal of Symbolic Computation, 38, 2004 - Newton polygons and families of polynomials
Manuscripta Mathematica, 113, 2004 - Irregular fibers of complex polynomials
Revista Matemàtica Complutense, 17, 2004 - Invariance of Milnor numbers and topology of polynomials
Commentarii Mathematici Helvetici, 78, 2003 - Non reality and non connectivity of polynomials
C. R. Acad. Sci. Paris, 335, 2002 - Classification of polynomials with one critical value
Mathematische Zeitschrift, 242, 2002 - Milnor fibration and fibered links at infinity
International Mathematics Research Notices (IMRN), 11, 1999
Others
Quelques contributions à la topologie et à l’arithmétique des polynômes
Habilitation Thesis, University Lille 1, July 2008
Les polynômes de plusieurs variables sont présents sous de nombreuses formes en géométrie. L’exemple qui vient immédiatemment à l’esprit est celui d’une courbe algébrique, définie comme le lieu des points qui annulent un polynôme…
- The memoir (in French)
- The articles presented (in English)
- The slides of the defense (in French)
Fibres et entrelacs irréguliers à l’infini
Ph.D. Thesis, University Toulouse 3, December 2000
- The relative Schinzel hypothesis
with P. Dèbes and S. Najib, preprint, 2020.
This paper is superseded by the new one: “The Hilbert-Schinzel specialization property”, with J. König. - Realization of intermediate links of line arrangements preprint that will not be submitted
Computations
-
roots_lib.sage, roots_examples.sage, roots_examples_article.sage A Sage library for computing efficiently the solutions of P(x) = 0 (mod p^e) using the trunk and and the tree. See the article Solutions of a polynomial equation modulo a prime power above.
-
root-1.mwf, root-2.mw, root-3.mw Maple sheets that compute the decomposition P = h(Q)+R firstly from a pratical point of view, secondly from the point of view of decomposable polynomials and affine equations of the set of all decomposable polynomials and finally for polynomials in two variables. See the article Decomposition of polynomials and approximate roots above.
-
count_th1.mw, count_th2.mw, count_th3.mw and count_th3_bis.mw Maple sheets that compute the number of irreducible and indecomposable polynomials over a finite field.
See the article Generating series for irreducible polynomials above. -
irredu.lib and irredu.mw A library and an example sheet for Maple that compute the number of irreducible polynomials over a finite field. See the article Number of irreducible polynomials above.
-
critic.lib A library for Singular that enables the computation of critical values (in affine space and at infinity) for polynomials in n variables. This library also compute Milnor numbers (in affine and at infinity) for critical fibers. See the article Computation of Milnor numbers and critical values at infinity above.
-
defpol.lib Another library for Singular that compute critical parameters in deformations of polynomials in n variables. See the article Computation of Milnor numbers and critical values at infinity above.
-
stein.lib A library for Singular that finds reducible fibers of a bivariate polynomial. Some explanations in Reducible fibers of polynomials
Last modification : October 2025